Precision of Estimates of Nonresponse Bias in Surveys

Abstract

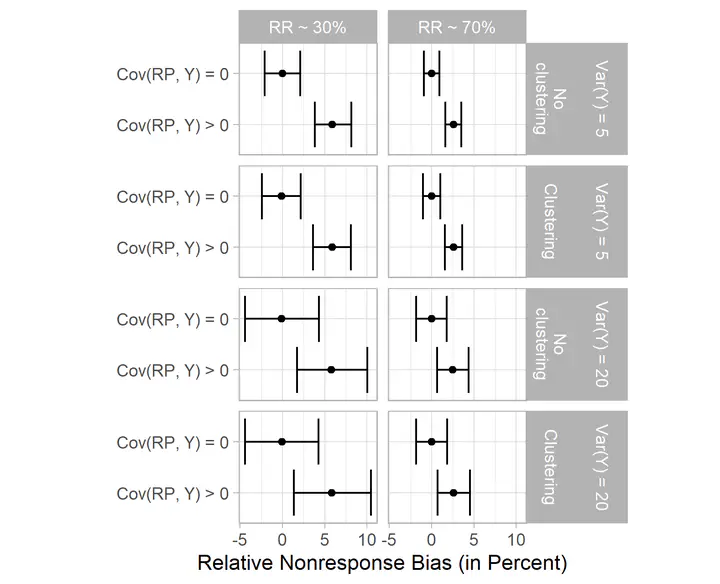
Survey data producers increasingly provide estimates of nonresponse bias in several variables when they release or analyze data. Researchers understand that sample estimates of population values should be reported with appropriate measures of uncertainty, such as standard errors or confidence intervals. However, few studies acknowledge that nonresponse bias estimates are also subject to sampling variability. Using simulations, we study the sampling variability of nonresponse bias estimates in means and how that variability is affected by features such as clustering and response rates. Results show that low response rates and high clustering make nonresponse bias estimates more variable. We then evaluate three methods to estimate the sampling variance for nonresponse bias estimates: a method developed by Lee (2006), jackknife replication, and linearization. We find that linearization and replication work well with all populations and give an algorithm for the implementation of these approaches. We also apply the Lee and replication methods to the LISS panel and the General Social Survey, confirming the simulation results.